近日,建工學院教師何濤在計算力學頂刊《Computer Methods in Applied Mechanics and Engineering》(中科院一區TOP期刊,JCR-Q1,IF = 6.9)發表題為“On the mesh insensitivity of the edge-based smoothed finite element method for moving-domain problems”的研究論文。文章針對時變域動網格破壞難題提出了一種高效便捷的光滑有限元改進方案,并成功用于各類流固耦合問題模擬。何濤是本文的獨立作者,上海師范大學為唯一署名單位。

復雜的運動域問題(如流固耦合)易引發有限元網格徹底破壞而致使數值計算失敗。因此,傳統有限元方法多用于中等幅度變形的流固耦合模擬。光滑有限元法是近二十年發展起來的一種新型方法,同時兼具有限元法和無網格法的優點,特別是對網格扭曲不敏感。然而,這一優勢當前還未被充分開發和利用。為此,本文研究提出一種基于破壞單元的邊線型光滑域構造措施,使之能夠正確計算極端網格扭曲下的瞬態動力方程。本文從數學上證明了原邊線型光滑有限元法面對網格扭曲的局限性和改進措施對動網格破壞的天然適應性。建議方法完全兼容常規方案且無需額外空間穩定措施,能無障礙運用于各類良好/扭曲/破壞網格,還可推廣至其它線性單元。審稿人認為,“The proposed method exhibits improved robustness, stability, and accuracy in complex moving-domain analyses. The manuscript provides new and interesting results.”。研究成果可望為保障復雜動邊界問題精確模擬提供一種新思路。
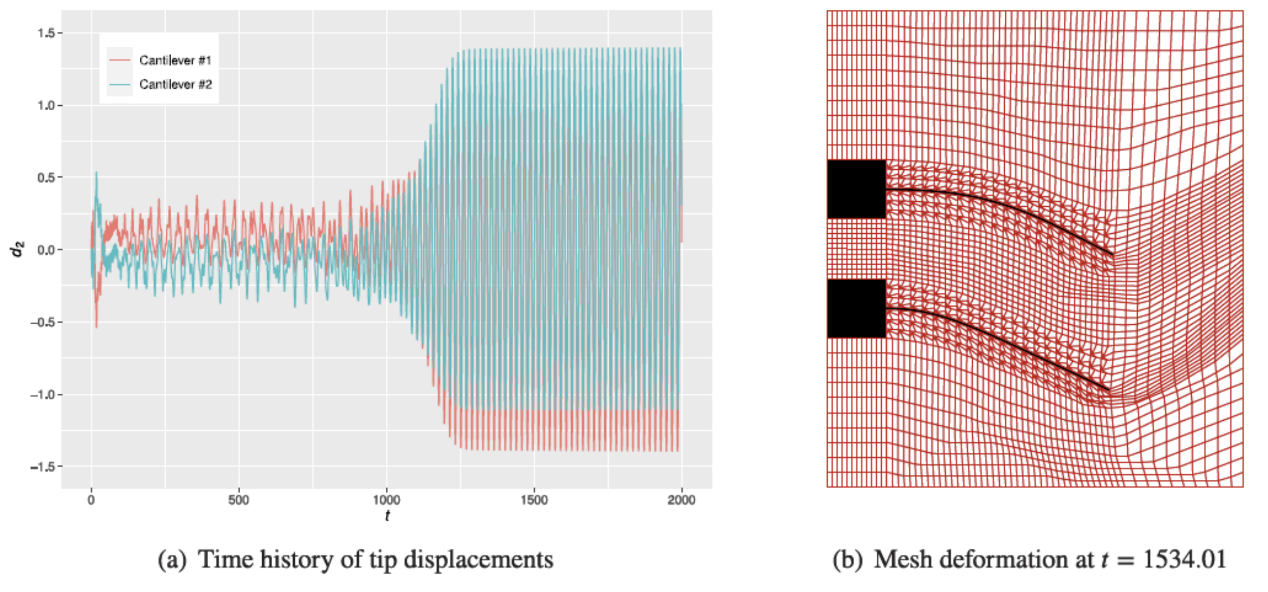
基于破壞網格的多體流固耦合精確模擬
何濤老師近年來持續聚焦流固耦合數值算法,取得了系統研究成果,相繼在《Computer Methods in Applied Mechanics and Engineering》《Journal of Computational Physics》和《International Journal for Numerical Methods in Engineering》三大計算力學頂刊上發表多篇高水平論文。部分研究成果已被有限元法經典教材《The Finite Element Method for Fluid Dynamics (Eighth Edition)》(O.C. Zienkiewicz,R.L. Taylor, P. Nithiarasu著,2024年11月)引用。
本文工作得到了國家自然科學基金面上項目的支持。全文鏈接網址:https://www.sciencedirect.com/science/article/pii/S0045782525001896
(供稿、圖片:建筑工程學院)












 徐匯校區:上海市徐匯區桂林路100號
徐匯校區:上海市徐匯區桂林路100號